The transformation problem

Intuitively (and I don't yet have the tools to analyze the problem mathematically) I suspect that the transformation problem might be "unsolvable", but the unsolvability might actually be evidence for a labor theory of value as a semi-normative theory, i.e. as a means to the end (or a way of measuring progress towards the end) of an efficient economy.

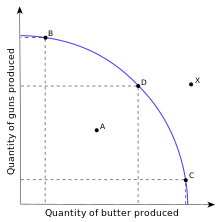
An efficient economy operates at the the production-possibility frontier, the trade-off between producing different combinations of various commodities. Any point on the frontier (the blue line in the graph to the right, e.g. points B, C and D) represents efficient aggregate production: we could not produce more of one commodity without sacrificing production of another. Any point "outside" the frontier (e.g. point X) is impossible to achieve given the current means of production. Any point "inside" the frontier (e.g. point A) represents real inefficiency: we could produce more of one commodity without sacrificing any production of the other.

The production-possibility frontier has direct implications on prices. The relative prices of the commodities when production is on the frontier should have some definite relationship to bind them to the line, but prices inside the frontier will not have that same relationship, since they are set inside an area, not on a line, giving them another degree of freedom.

Suppose, for example, we impose a "tax" on butter, and this tax is simply wasted. For every nine workers a butter manufacturer hires, he must hire another worker at the same wage to sit around watching TV and surfing the net. This "tax" then reduces whatever level of butter production we might achieve without achieving a corresponding increase in the number of guns produced. Since we could (by not paying 10% of our butter production workforce to sit around doing nothing) produce more guns without producing less butter, we must therefore be inside the production-possibility frontier, and our economy is not efficient.

The relative prices of guns and butter, however, will have some definite relationship that takes into account this wasted tax on butter. Having this relationship, however, based on inefficient production means that any relationship with the assumption of efficient production will not hold.

My speculation is that the requirement that capital receive a constant rate of return by itself introduces real economic inefficiency. Furthermore, because a capitalist economy typically measures total rate of return on capital, but the real rate of return is a rate on variable capital (the surplus value of the workers), the economic inefficiency is not just variable across industries with different organic compositions of capital, but it's also opaque.

To sum up: At the production-possibility frontier, the labor theory of value should more-or-less obviously hold. The requirement of a constant rate of return on total capital places us inside the production-possibility frontier. The inefficiencies introduced by the constant rate of return will vary according to the organic composition of capital. We could solve the transformation problem only by measuring the individual organic compositions; since these values are opaque, the transformation problem is unsolvable. Observing that the labor theory of value does not more-or-less obviously hold (and the transformation problem is unsolvable) is direct evidence that the economy is not efficient.

Is it true? I dunno. Ask me in a few years when this is my PhD thesis topic.